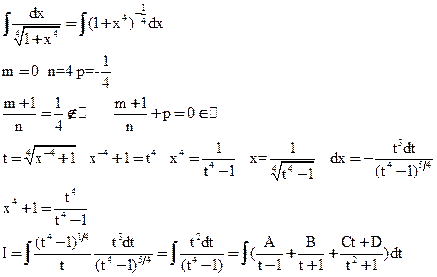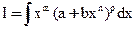Языки программирования
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С
Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование
Все о программировании
Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации
Дата добавления: 2015-09-15; просмотров: 3386; Нарушение авторских прав
- дифференциальный бином
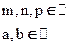
Интегрируется в трёх случаях
1 случай
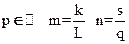
Приведём дроби m и n к общему знаменателю
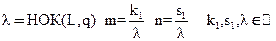
Замена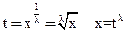
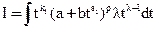- интеграл от рациональной функции
2 случай
Преобразуем интеграл 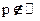. Замена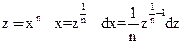
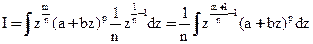
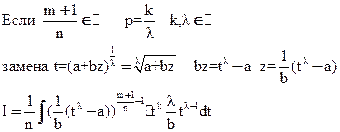
Получили интеграл от рациональной функции
3 случай z=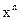
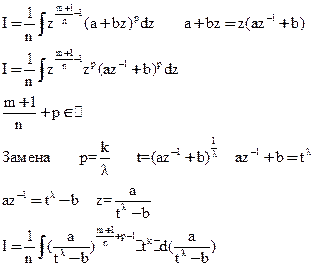
Получили интеграл от рациональной функции (подстановка Чебышева)
Вывод: интеграл 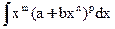рационализуется, если:
1) 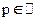замена 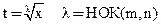( общей знаменатель дробей m и n )
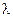2) где - знаменатель дроби p
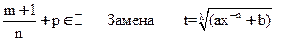
3) 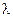- знаменатель дроби p
Пример
Карта сайта Карта сайта укр
Аппаратное и программное обеспечение Графика и компьютерная сфера Интегрированная геоинформационная система Интернет Компьютер Комплектующие компьютера Лекции Методы и средства измерений неэлектрических величин Обслуживание компьютерных и периферийных устройств Операционные системы Параллельное программирование Проектирование электронных средств Периферийные устройства Полезные ресурсы для программистов Программы для программистов Статьи для программистов Cтруктура и организация данных
Не нашли то, что искали? Google вам в помощь!
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна.
- дифференциальный бином
- интеграл от рациональной функции
. Замена 
рационализуется, если:
замена 
( общей знаменатель дробей m и n )
где 
- знаменатель дроби p
