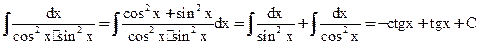Определение

Неопределённый интеграл.

Определение и свойства неопределённого интеграла

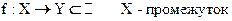
Определение

Функция F(x) называется первообразной f(x) на X, если:

1) F(x) – дифференцируема в каждой внутренней точке X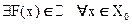

2)

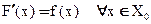
Пример

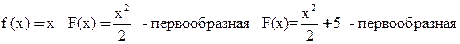
Вывод: Если нашлась одна первообразная F(x) для функции f(x), то F(x)+C так же будет первообразной для функции f(x).

Лемма

Пусть F(x) и Ф(x) – две различные первообразные f(x) на промежутке X.

Тогда F(x) - Ф(x) = С

Доказательство:

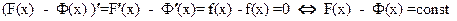
(из теорему об условии постоянства функции на промежутке)

Вывод: Если F(x) – некоторая первообразная функции f(x), то F(x)+C – множество всех первообразных.

Определение

Неопределённый интеграл от функции f(x) – множество всех первообразных для функции f(x)

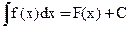, С – любое действительное число

Свойства неопределённого интеграла:

1)

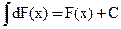
Доказательство:

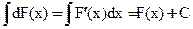
2)

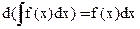
Доказательство:

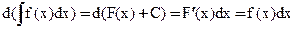
Первые два свойства говорят о том, что дифференцирование и интегрирование - взаимно обратные операции.

3)

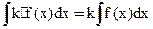
Доказательство:

Пусть F(x) - первообразная f(x), тогда kF(x) - первообразная от kf(x)

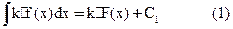
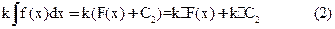
Так как С₁ и С₂ – произвольные константы, то (1)=(2)

4)

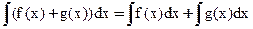
Доказательство:

Пусть F(x) – первообразная f(x)

G(x) – первообразная g(x), тогда

F(x)+G(x)- первообразная f(x)+g(x)

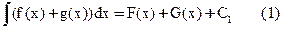
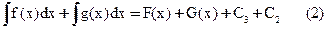
Так как С₁ С₂ С₃ - произвольные константы то (1)=(2)

Таблица интегралов

1)

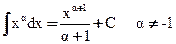
2)

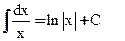
3)

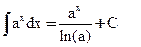
4)

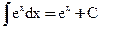
5)

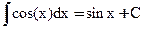
6)

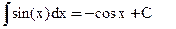
7)

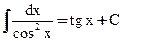
8)

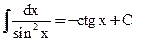
9)

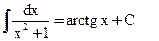
10)

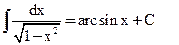
11)

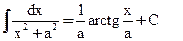
12)

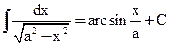
13)

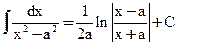
14)

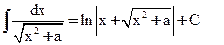
15)

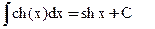
16)

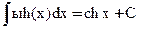
17)

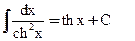
18)

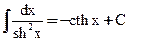
Пример

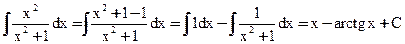
Пример

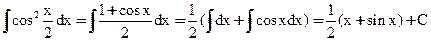
Пример