Интегрирование по частям

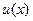Пусть и 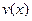- непрерывно дифференцируемые функции от 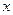, тогда:

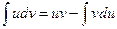
Порядок вычислений:

1) все подынтегральное выражение разбить на две части: одну обозначить через 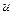, другую – через ;

2) вычислить дифференциал от функции по формуле и функцию 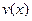, интегрируя ;

3) применить формулу интегрирования по частям;

4) вычислить интеграл и записать окончательный ответ.