Этот прием представляет сведение данного интеграла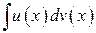 
к интегралу 
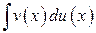с помощью формулы
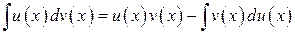
Этот прием ведет к цели, если 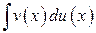находится легче, чем .
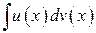Это правило хотя и имеет более ограниченную область применения по сравнению с заменой переменной, существует целый класс функций, который интегрируется именно с помощью этого метода. Сюда можно отнести:
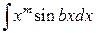
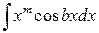
где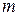 
- целое положительное число. Применение метода интегрирования по частям предусматривает последовательное понижение степени 
до нулевой.
Примеры:
2.2.1. Найти интеграл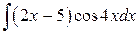 
.
n Применим формулу интегрирования по частям, обозначив
, 
, 
, 
.
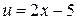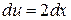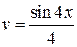Тогда
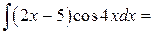
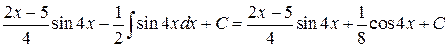ƒ
2.2.2. Найти интеграл: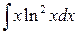 
n Применяя дважды интегрирование по частям
В первый раз, обозначим: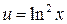 
, 
, 
, 
, получим
,
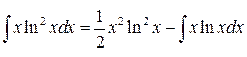а во второй раз: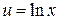 
, , 
, , получаем:
ƒ
2.2.3. Найти интеграл: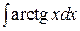 
n Обозначая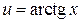 
, 
, 
, 
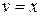и применив в ходе вычисления замену 
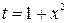, получим
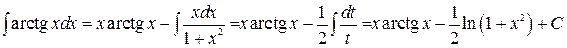ƒ
2.2.4. Найти интеграл: 
■ Применим метод интегрирования по частям:
.◄
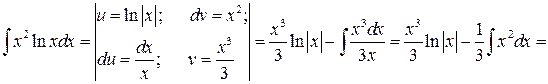
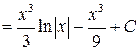2.2.5. Найти интегралы: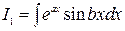 
и 
.
■ Применим метод интегрирования по частям:
;
.
Таким образом, получается система линейных уравнений относительно неизвестных 
и 
:
,
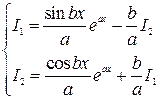разрешая которую, получаем
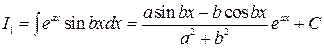
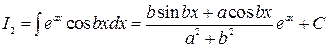.ƒ
