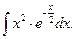Если u и v – дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций
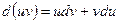, откуда
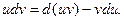
Интегрируя обе части последнего равенства , получим:
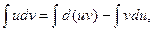или
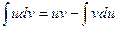. (1)
Это и есть формула интегрирования по частям.
Укажем некоторые часто встречающиеся интегралы, которые вычисляются методом интегрирования по частям.
1. Интегралы вида
; 
; 
,
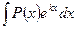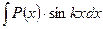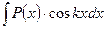где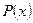 
- многочлен, 
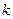- некоторое число.
За u принимают 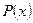, т. е.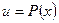 
2. Интегралы вида
; 
; 
; 
; 
,
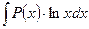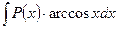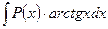где 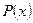- многочлен. Во всех этих случаях за u принимают функцию, являющуюся множителем при .
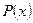3. Интегралы вида
; 
,
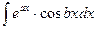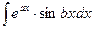где а и в – числа, находятся двукратным интегрированием по частям.
Пример 1. Найти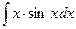 
.
Решение. Обозначим: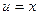 
; 
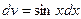
Для применения формулы (1) необходимо знать ещё du и v . Дифференцируя равенство 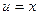, получаем 
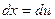. Интегрируем 
, 
.
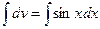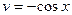Подставляя значения u, v, du, dv в формулу (1), находим
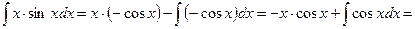
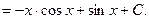
Пример 2. Найти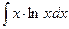 
Решение. Полагая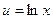 
, 
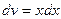, получаем 
; 
.
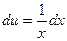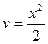По формуле (1) находим
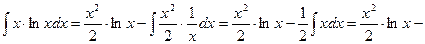
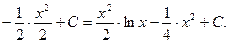
Пример 3. Найти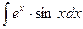 
Решение. Положим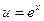 
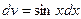, , отсюда 
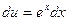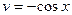, . Тогда
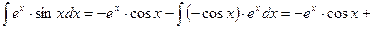
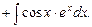(2)
К интегралу в правой части снова применяем формулу интегрирования по частям.
Положим ,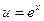 
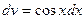, отсюда , 
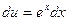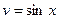. Тогда
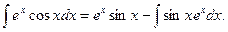
Подставляем найденное выражение в равенство (2), получаем
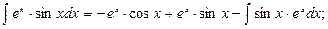
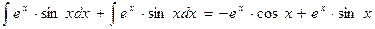
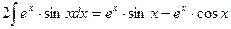
следовательно,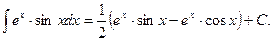 
Задачи. Найти неопределенные интегралы:
1. 
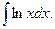
2. 
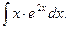
3. 
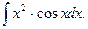
4. 
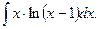
5. 
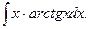
6. 
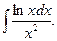
7. 
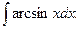
8. 
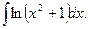
9. 
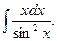
10. 
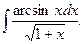
11. 
12. 
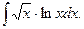
13. 
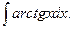
14. 
15. 
