1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
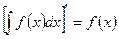 ,
, 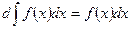 .
.
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
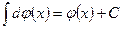 .
.
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
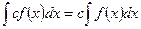
 .
.
Для доказательства данного равенства найдем производные от левой и правой частей:
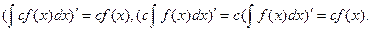
Производные от правой и левой частей равны, следовательно разность двух любых функций ,стоящих слева и справа ,есть постоянная. В этом смысле и следует понимать данное равенство.
4. Неопределенный интеграл от алгебраической суммы непрерывных функций равен такой же алгебраической сумме неопределенныx интегралов от слагаемых:
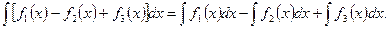
При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила.
- Если
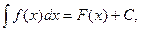 то
то
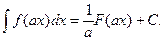
- Если
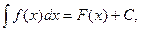 то
то
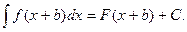
- Если
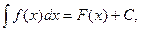 то
то
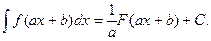
Таблица основных интегралов.
1. 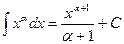 .
. 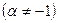
2. 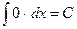 .
.
3. 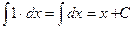 .
.
4. 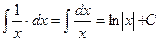 .
. 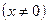
5. 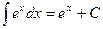 .
.
6. 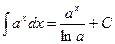 .
.
7. 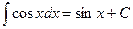 .
.
8. 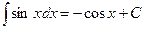 .
.
9. 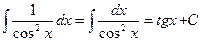 .
.
10. 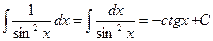 .
.
11. 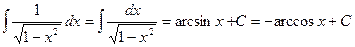 .
.
12. 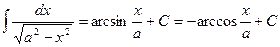 .
.
13. 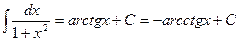 .
.
14. 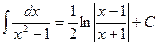 .
.
15. 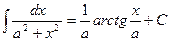 .
.
16. 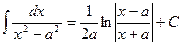 .
.
17. 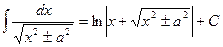 .
.
18. 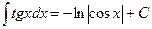 .
.
19.  .
.
20. 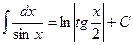 .
.
21. 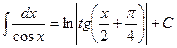 .
.