Биномиальным дифференциалом называют выражение вида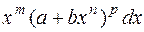 
, где 
, 
– действительные числа, а показатели степени 
, 
, 
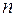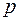– рациональные числа.
Выясним случаи, когда подобные выражения рационализируются.
IV.1 
. Этот случай соответствует ситуации, рассмотренной в пункте I. Действительно,
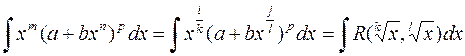
и интеграл рационализируется подстановкой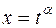 
, где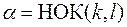 
.
IV.2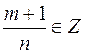 
. Рассмотрим подстановку 
, где 
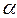– знаменатель дроби 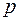, так что 
. Тогда 
, 
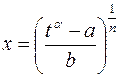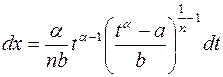и
.
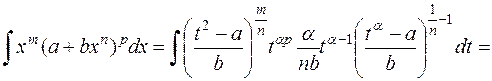
IV.3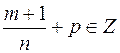 
. Предлагается подстановка 
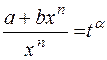, где 
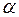– знаменатель дроби 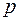. Докажите самостоятельно, что и в этом случае, интеграл рационализируется.
Эти три случая интегрируемости биномиальных дифференциалов в элементарных функциях были известны еще в XVII веке. Однако, лишь в XIX веке Чебышев доказал, что других случаев нет.
Пример 6. 
.
Здесь 
, 
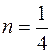и 
; так как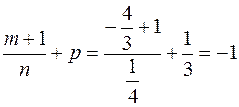 
, то имеем случай третьей подстановки Чебышева. Итак,
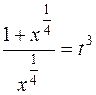или 
.
Находим отсюда 
и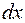 
:
, 
, 
, 
.
Кроме того,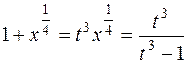 
. Имеем для интеграла:
.
