Интеграл вида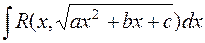 
выделением полного квадрата в подкоренном выражении и соответствующей заменой переменной можно свести к одному из интегралов, рассмотренных ранее.
Однако, существуют и прямые способы рационализации интеграла – это так называемые подстановки Эйлера. Новая переменная интегрирования 
вводится такими соотношениями:
1) если 
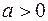, то 
;
2) если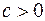 
, то 
;
3) если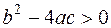 
, то 
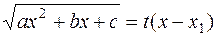, где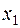 
– один из корней квадратного трехчлена.
Возводя эти соотношения в квадрат и упрощая, можно убедиться в том, что 
, 
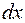и радикал 
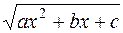выражается через рациональным образом. Следовательно, данный интеграл рационализируется.
Предлагается студентам самостоятельно произвести все необходимые преобразования и применить эти подстановки к вычислению интегралов:
, 
, 
.
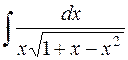