В этой части параграфа рассмотрим интегралы вида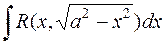 
и 
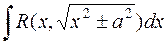. В этих интегралах удается избавиться от иррациональности с помощью тригонометрических или гиперболических подстановок, после чего рационализировать интеграл подстановками, рассмотренными в предыдущем параграфе.
II.1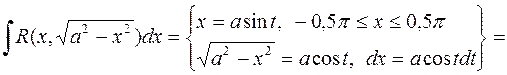 
.
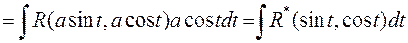С тем же успехом можно взять и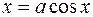 
, 
.
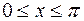II.2
a)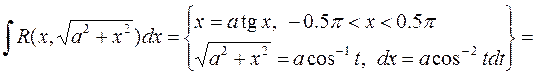 
;
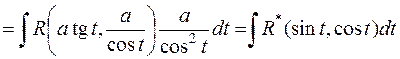b)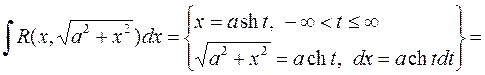 
.
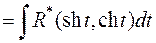II.3
a)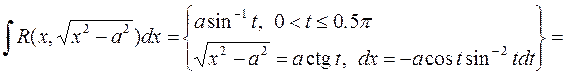 
;
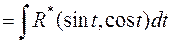b)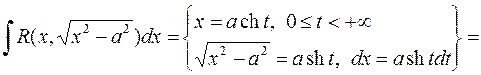 
.
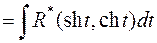Относительно интеграла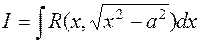 
необходимо сделать следующее замечание. Область определения радикала 
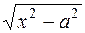состоит из 2-х частей: 
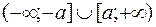. Рассмотренные выше замены справедливы лишь 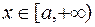для 
. Для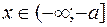 
тригонометрическая замена та же, но 
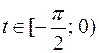и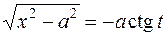 
, а гиперболическая замена имеет вид 
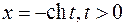. В случае четной или нечетной подынтегральной функции можно пользоваться соответствующими свойствами первообразных (см. §1) и не рассматривать отдельно случай 
.
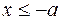Примеры.
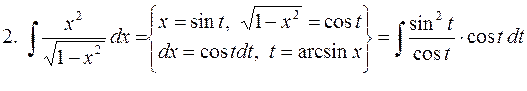
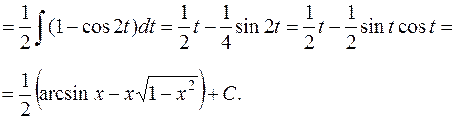
3. 
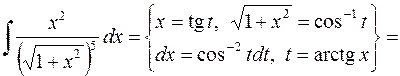
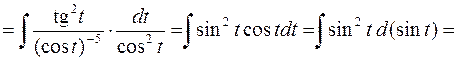
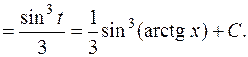
Если учесть, что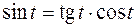 
, то ответ можно упростить
.
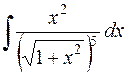
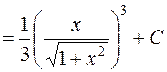4. 
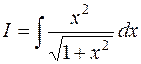. Здесь тригонометрическая замена приведет к сложно-му интегралу 
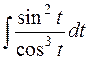, поэтому лучше применить гиперболическую подстановку: 
, 
, 
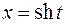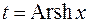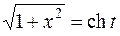. Имеем
.
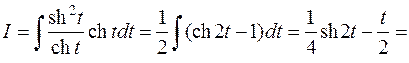
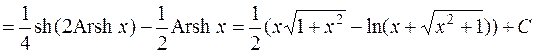Здесь на последнем шаге использована формула для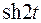 
и выражение 
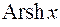через логарифм.
5. 
.
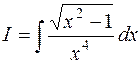Для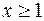 
сделаем замену 
, 
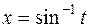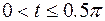, тогда 
, 
, 
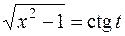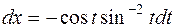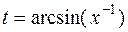и получим
.
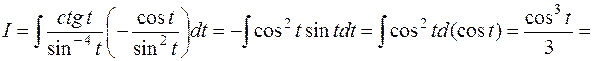
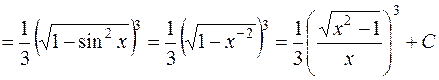Подынтегральная функция – четная, а полученная первообразная нечетная, значит результат справедлив и для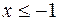 
.
