Правило III §3 позволяет сразу написать
,
.
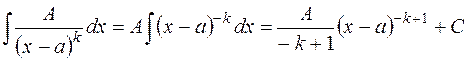Чтобы проинтегрировать дроби третьего и четвертого типов, следует выделить полный квадрат, сделать замену переменной и разбить интеграл на сумму двух интегралов. Например, для дроби третьего типа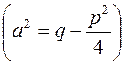 
:
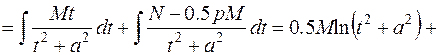
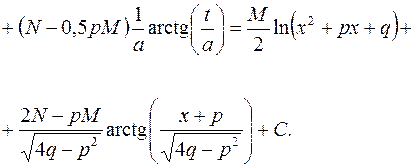
Для дроби четвертого типа аналогично будем иметь
Здесь интеграл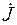 
вычисляется путем подведения под знак дифференциала:
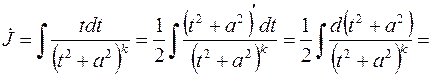
Для интеграла во втором слагаемом можно вывести рекуррентную формулу, предварительно преобразовав его следующим образом:
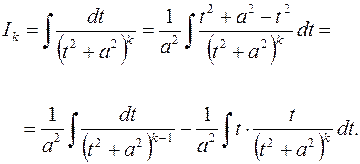
Ко второму интегралу применим формулу интегрирования по частям, положив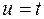 
, 
. Тогда 
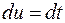, а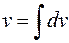 
– это уже вычисленный интеграл 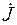. Получим
,
.
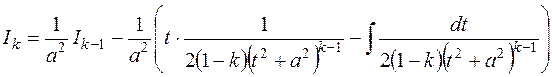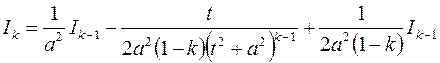Из последнего равенства и получим рекуррентную формулу
.
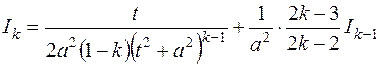Эта формула позволяет последовательно вычислять интегралы 
для любого 
, опираясь на то, что
.
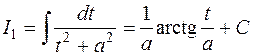Вывод: интегралы от простейших рациональных дробей выражаются в конечном виде через рациональные дроби, логарифмы и арктангенсы.
