В этом параграфе рассматриваем интегралы вида
, 
.
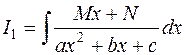В квадратном трехчлене выделим полный квадрат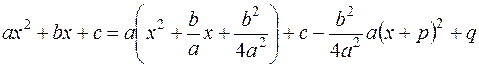 
, где 
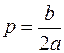, а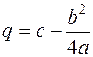 
. После этого интеграл можно разбить на сумму двух интегра-
лов. Например,
.
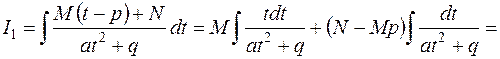
Интеграл в первом слагаемом – это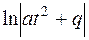 
, а во втором – арктангенс или «высокий» логарифм.
Аналогично для 
получим:
.
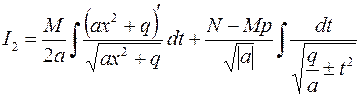Здесь первый интеграл равен 
, а второй – это арксинус или «длинный» логарифм.
Примеры.
1. 
.
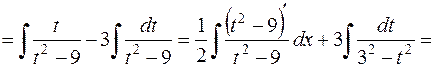
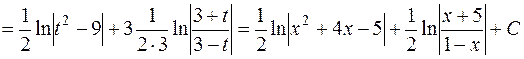2. 
.
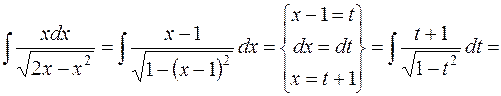
Замечание. Если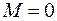 
, то интегралы 
и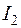 
после выделения полного квадрата можно найти с помощью правила III из §3 (замена переменной не обязательна).
