Теорема 3. Если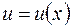 
и 
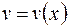– непрерывно-дифференци-руемые функции, то справедлива формула
. (4)
Доказательство вытекает из правила дифференцирования произведения: 
. Проинтегрируем обе части этого равенства и учтем одно из свойств неопределенного интеграла:
,
,
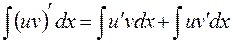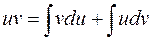отсюда и следует формула интегрирования по частям (3).
При практическом применении этого метода подынтегральное выражение надо разбить в произведение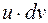 
таким образом, чтобы функция 
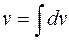вычислялась просто, а интеграл в правой части (4) был бы проще исходного.
Примеры.
10. 
.
.
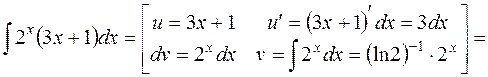
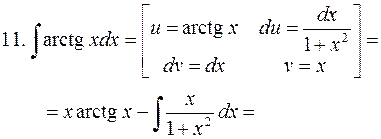
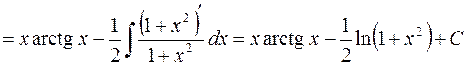Замечание 3. Если при вычислении интеграла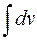 
взять другую первообразную, например 
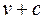, получим тот же результат:
.
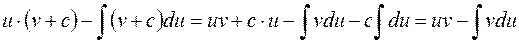Замечание 4. Область применения этого метода в основном исчерпывается интегралами вида 
, где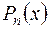 
– многочлен, а 
– это: 1) показательные, тригонометрические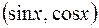 
и гипербо-лические функции; 2) логарифмические и обратные тригонометрические функции. При этом в качестве в случае 1) берем многочлен, а в случае 2)– логарифмы и аркфункции. Отметим, что в случае 2) «многочлен» может содержать степени переменной с ненатуральными показателями.
Примеры.
12. 
.
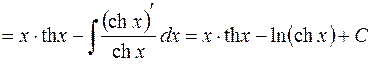13. 
.
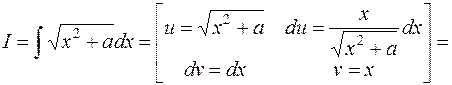
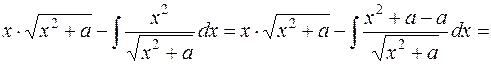
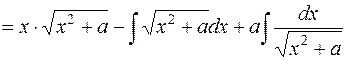Мы пришли к уравнению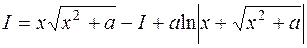 
, из которого
получаем
.
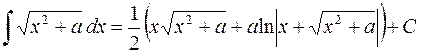14.Для интеграла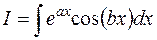 
путем двукратного интегриро-
вания по частям можно получить уравнение
,
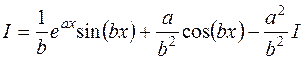из которого находим
.
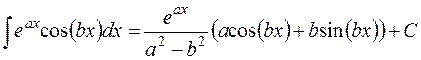Аналогичным образом можно найти интегралы
, 
, 
.
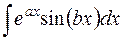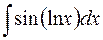