Теорема 2. Пусть требуется вычислить интеграл 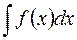 и пусть
и пусть 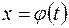 – непрерывно-дифференцируемая функция, имеющая обратную
– непрерывно-дифференцируемая функция, имеющая обратную 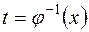 . Тогда, если
. Тогда, если
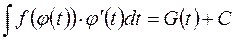 , (2)
, (2)
то
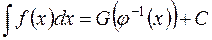 . (3)
. (3)
Доказательство. Равенство (2) означает, что 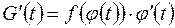 . Тогда
. Тогда
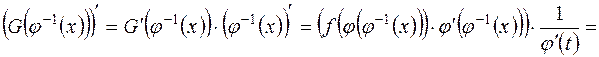
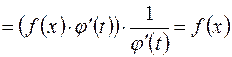 .
.
Сравнение начала и конца этой цепочки равенств и доказывает равенство (3).
Пример.
9. 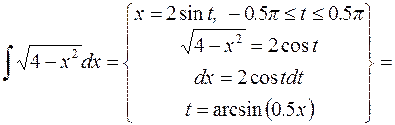
= 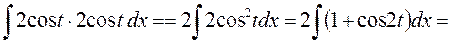
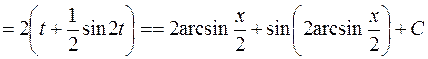 .
.
Ответ можно упростить, если учесть формулу синуса двойного угла:
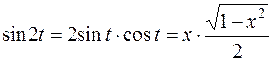 .
.