Теорема 1. Пусть известно, что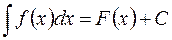 
. Тогда, если функция 
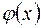– непрерывно-дифференцируема, то
. (1)
Доказательство. Первое условие теоремы означает, что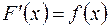 
.
Применяя правило дифференцирования сложной функции, получим
,
что и доказывает (1).
Чтобы воспользоваться этой теоремой на практике, необходимо вычленить в подынтегральной функции производную некоторой функции, объединить эту производную с дифференциалом переменной интегрирования и сделать замену. После вычисления интеграла вернуться к исходной переменной интегрирования.
Примеры.
6. 
.
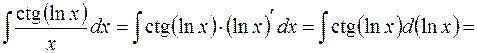
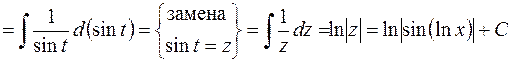Замечание 1. Замену такого типа можно производить и без подведения под знак дифференциала.
7. 
.
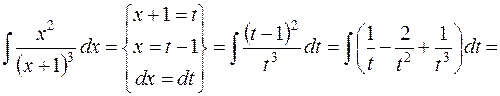
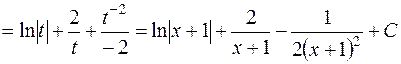8. 
.
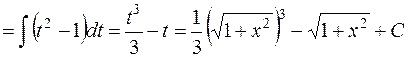Сразу отметим здесь, что такой простой заменой не всегда удается избавить-
ся от иррациональности (попробуйте сами, заменив в числителе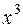 
на 
).
Замечание 2. Приведем две формулы, которые часто встречаются и их
лучше запомнить как табличные:
,
.
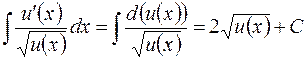