Теорема 2. Если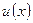 
и 
- дифференцируемые функции, то
или
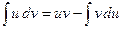. (3)
Формула (3) называется формулой интегрирования по частям для неопределенного интеграла.
Можно выделить следующие типы интегралов, для нахождения которых используется формула интегрирования по частям:
I. 
, 
, 
.
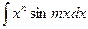II. 
, 
, 
, 
, 
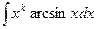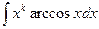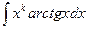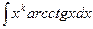, где 
и 
- целое положительное число.
Для нахождения интегралов из первой группы полагаем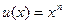 
, а остальные сомножители подынтегральной функции задают 
.
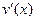Для интегралов из второй группы полагаем 
, а а остальные сомножители подынтегральной функции задают 
.
Пример 5.
1) Вычислим интеграл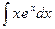 
. Пусть 
, тогда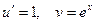 
. По формуле (3) получаем, что 
.
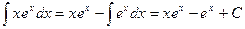Следующие интегралы вычисляются подобным же образом.
2) 
.
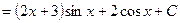3) 
.
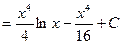4) 
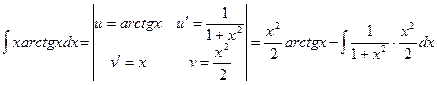, так как 
, то 
.
5) 
. Для последнего интеграла снова используем метод интегрирования по частям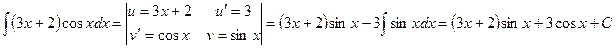 
. Окончательно получаем, что 
.
6) Рассмотрим еще один пример, где комбинируются два метода.
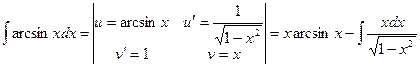. В последнем интеграле сделаем замену 
(можно и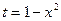 
), тогда 
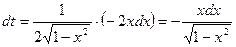. Следовательно, 
. Окончательно получаем, что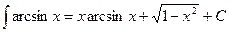 
.
