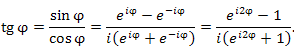Пусть 
. Положим 
, 
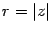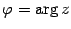. Из рисунка 17.4 очевидно, что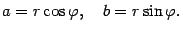 
Тогда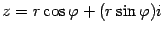 
. Это выражение запишем в виде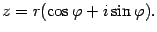 
Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде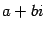 
называют иногда алгебраической формойкомплексного числа. Отметим, что тригонометрическая форма -- это указание числа по двум его характеристикам: модулю и аргументу. Поэтому вместо формулы (17.8) можно было бы просто записывать пару 
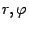, но запись (17.8) принята в силу традиции.
35 Формула Эйлера
устанавливает взаимосвязь между экспоненциальной функцией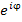 
и тригонометрическими функциям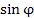и 
и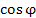 
на множестве комплексных чисел: 
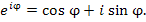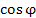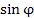Доказательство формулы Эйлера основано на представлении этих функций в виде степенных рядов и при первом чтении может быть опущено без ущерба для понимания последующего изложения. Заметим, что и представляют собой соответственно вещественную и мнимую части экспоненциальной функции : 
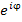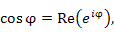
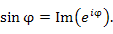Выполним в формуле Эйлера замену 
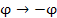: Выполнив почленное сложение и вычитание выражений в обеих частях равенств (1) и (3), получим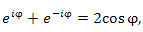 
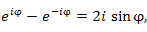что влечет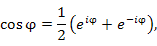 
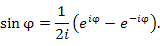Таким образом, тригонометрические функци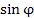и и 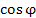представлены в виде линейных комбинаций экспоненциальных функци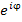й и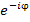 
. Тангенс аргумента φ выражается через 
: 
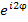