|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Применение дифференциала в приближенных вычисленияхДата добавления: 2015-01-16; просмотров: 1098; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

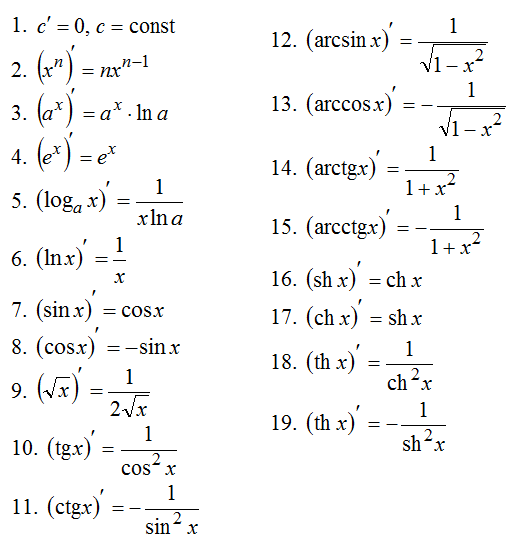
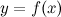 дифференцируема в точке
дифференцируема в точке  , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно 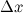 и нелинейного членов:
и нелинейного членов: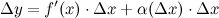 где
где 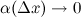 при
при 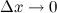 .
. Дифференциалом функции называется линейная относительно
Дифференциалом функции называется линейная относительно 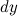 или
или 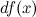 . Таким образом:
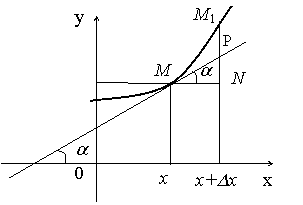
. Таким образом: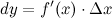 На графике функции
На графике функции 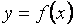 возьмем произвольную точку
возьмем произвольную точку 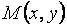 и дадим аргументу
и дадим аргументу  приращение
приращение 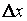 . При этом функция получит приращение
. При этом функция получит приращение 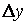 (на рисунке отрезок
(на рисунке отрезок  ). Проведем касательную к кривой
). Проведем касательную к кривой 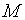 и обозначим угол ее наклона к оси
и обозначим угол ее наклона к оси 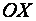 через
через 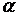 , тогда
, тогда 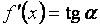 . Из треугольника
. Из треугольника 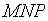 находим
находим 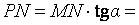
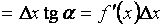 , т.е.
, т.е. 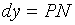 . Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции
. Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции 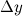 функции
функции 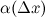 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента 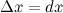 , то
, то 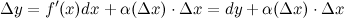 В силу того, что второе слагаемое
В силу того, что второе слагаемое 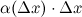 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому 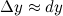 тА так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике. Для приближенного вычисления значения функции применяется следующая формула:
тА так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике. Для приближенного вычисления значения функции применяется следующая формула: 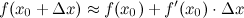
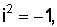
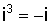 ,
, 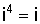 и т. д. Суммой двух комплексных чисел
и т. д. Суммой двух комплексных чисел 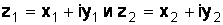 называется число
называется число  такое, что справедливы равенства
такое, что справедливы равенства 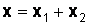 ,
, 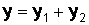 , т. е.
, т. е. 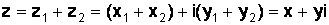 .
. .Правило сложения. При сложении комплексных чисел складываются действительные и мнимые части соответственно.
.Правило сложения. При сложении комплексных чисел складываются действительные и мнимые части соответственно.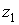 и
и 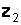 , где
, где 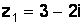 ,
,  Решение.
Решение. 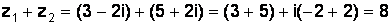 .
.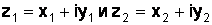 называется число
называется число 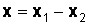 ,
, 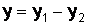 , т.е.
, т.е. 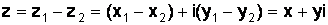 .
. . Правило вычитания. При нахождении разности комплексных чисел из действительной и мнимой частей уменьшаемого
. Правило вычитания. При нахождении разности комплексных чисел из действительной и мнимой частей уменьшаемого 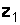 вычитаются соответственно действительная и мнимая части вычитаемого.
вычитаются соответственно действительная и мнимая части вычитаемого.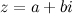 будет однозначно соответствовать на комплексной плоскости точка
будет однозначно соответствовать на комплексной плоскости точка 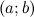 :
: 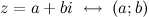 (рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.
(рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой - мнимая.