Определение 1. Функция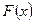 
называется первообразной для функции 
на множестве 
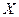, если 
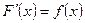для всех 
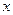из .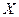
Пример 1.
1) 
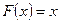первообразная для 
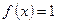, так как 
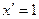. Аналогично, 
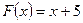также первообразная для 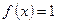, потому что 
.
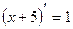2) 
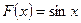первообразная для 
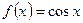, так как 
.
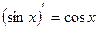Свойства первообразных.
1. Если 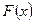- первообразная для , то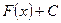 
также первообразная для .
2. Есл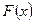и и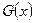 
- две первообразные для функции , то существует константа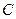 
такая, что
.
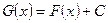Свойства 1 и 2 можно объединить в одно следующим образом.
3. Множество всех первообразных функции имеет вид: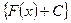 
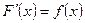, где , а 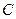- произвольное число.
Определение 2. Неопределенным интегралом от функции называется множество всех первообразных функции .
Неопределенный интеграл обозначается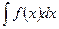 
, где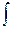 
- знак интеграла, - подынтегральная функция,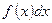 
- подынтегральное выражение.
Таким образом,
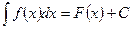, (1)
где 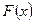- некоторая первообразная для , 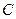- произвольная постоянная.
Пример 2. По определению 2 и примеру 1 имеем: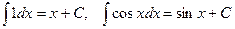 
.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
