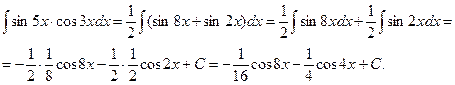П. 1. Универсальная тригонометрическая подстановка
Пусть 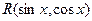 - рациональная функция от sin x и cos x. Тогда вычисление
- рациональная функция от sin x и cos x. Тогда вычисление 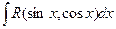 сводится к вычислению интеграла от рациональной функции подстановкой
сводится к вычислению интеграла от рациональной функции подстановкой 
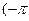 <x<
<x< 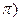 , которую называют универсальной тригонометрической подстановкой, так как
, которую называют универсальной тригонометрической подстановкой, так как
 ,
,
 ,
,  ,
,  .
.
Поэтому
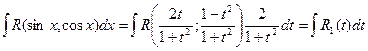 ,
,
где - 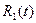 - рациональная функция от t.
- рациональная функция от t.
Пример. Найти 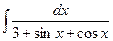 .
.
Обозначим  . Тогда
. Тогда 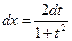 ,
, 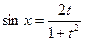 ,
, 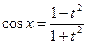 Þ
Þ

Замечание. На практике для рациополизации 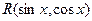 удобны следующие приемы рационализации:
удобны следующие приемы рационализации:
1) если 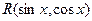 нечетна относительно sin x, т.е.
нечетна относительно sin x, т.е.
 , то полагают
, то полагают  ;
;
2) если 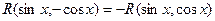 , то полагают
, то полагают  ;
;
3) если 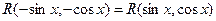 , т.е.
, т.е. 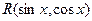 - четная функция относительно cos x и sin x, то полагают
- четная функция относительно cos x и sin x, то полагают 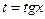 . Эта подстановка применяется и когда
. Эта подстановка применяется и когда 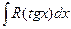 .
.
Примеры. 1) Найти  .
.
Так как 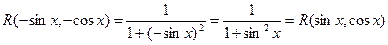 , то полагаем
, то полагаем 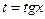 ®
® 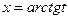 ,
,  ,
, 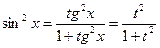 . Поэтому
. Поэтому
 .
.
2) 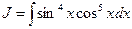
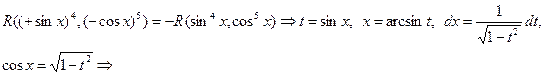
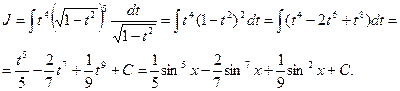
П. 2. Интегралы вида  ,
, 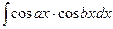 ,
,  вычисляются с помощью известных формул из тригонометрии:
вычисляются с помощью известных формул из тригонометрии:

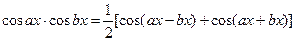
 .
.
Пример.