A. 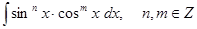 .
.
Теорема. Используя следующие подстановки, данный интеграл можно свести к интегралу от дробно-рациональной функции.
1. Если  - нечетное, то подстановка
- нечетное, то подстановка 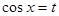 .
.
2. Если 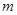 - нечетное, то подстановка
- нечетное, то подстановка 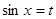 .
.
3. Если 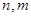 - четные, то подстановка
- четные, то подстановка 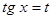 .
.
Если 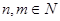 , то, используя тригонометрические тождества, интеграл можно преобразовать к сумме (разности) простейших интегралов.
, то, используя тригонометрические тождества, интеграл можно преобразовать к сумме (разности) простейших интегралов.
Примеры.
1) 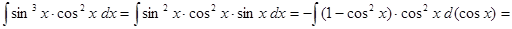
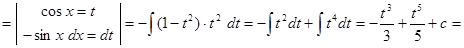
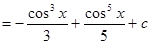 .
.
2) 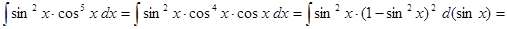
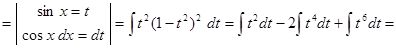
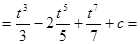
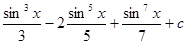 .
.
3) 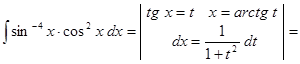
При замене 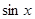 и
и 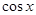 используются следующие формулы:
используются следующие формулы:
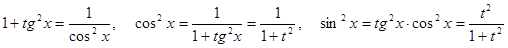 .
.
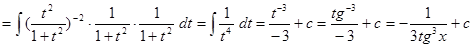 .
.
4) 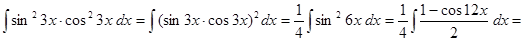
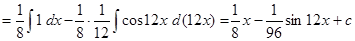 .
.
B. 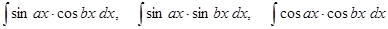
Данные интегралы преобразуются к простым с помощью тригонометрических формул.
Пример. 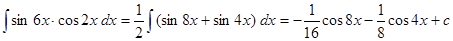 .
.
C. 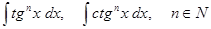 .
.
Рассмотрим интеграл
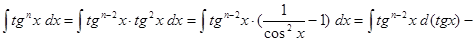
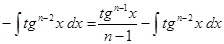 .
.
Повторяя этот прием несколько раз, мы постепенно уменьшаем показатель у тангенса. В результате, на каком-то шагу:
1. если  - четное, то получим
- четное, то получим 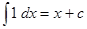 ;
;
2. если  - нечетное, то получим
- нечетное, то получим 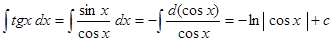 .
.
Пример. 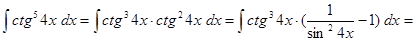
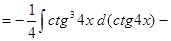
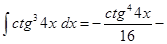
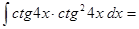
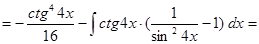
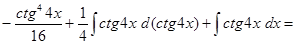
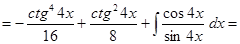
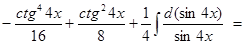
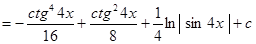 .
.
D. Универсальная подстановка.
Теорема. Интеграл 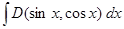 подстановкой
подстановкой 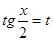 сводится к интегралу от дробно-рациональной функции.
сводится к интегралу от дробно-рациональной функции.
Пусть 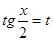 , выразим
, выразим 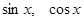 через
через 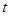 :
:
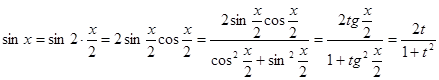 ,
,
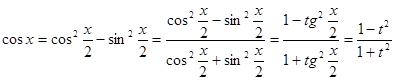 .
.
Пример. 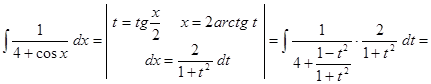
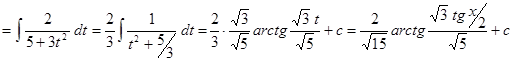 .
.