1. Интегрирование дроби 1-го типа. 
.
2. Интегрирование дроби 2-го типа.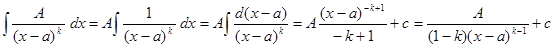 
.
3. Интегрирование дроби 3-го типа. 
По условию 
, выделим в знаменателе полный квадрат: 
т.к.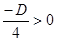 
, то это выражение можно обозначить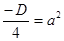 
,
.
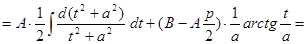
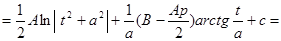
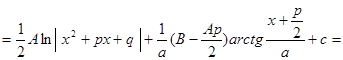
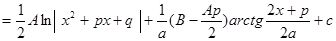4. Интегрирование дроби 4-го типа.
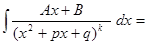
Проведя действия, аналогичные предыдущему пункту, получим:
.
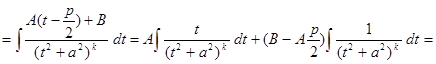
Рассмотрим способ вычисления интеграла 
. С помощью метода
интегрирования по частям сведем его к интегралу 
.
.
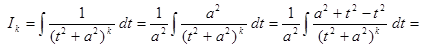
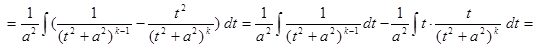
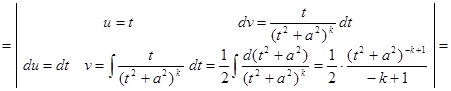
Полученная формула
называется рекуррентной. Применяя эту формулу к интегралу ,
сведем его к интегралу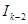 
, продолжая этот процесс, мы придем к 
.
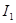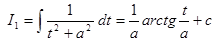. Следовательно, интеграл выразится
через сумму дробей и арктангенс. Т.к. можно вычислить, то и
интеграл от дроби 4-го типа будем считать вычисленным.
Пример. Вычислить интеграл 
Воспользуемся результатом примера
.
Последний интеграл вычислим отдельно:
.
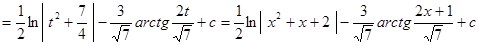Следовательно, исходный интеграл
= 
+ 
.
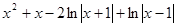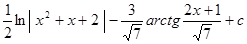Пример. Вычислить интеграл
.
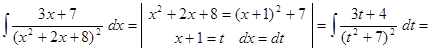
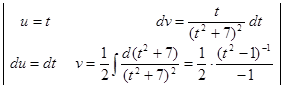
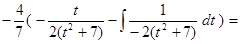
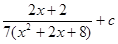Теорема. Интеграл от любой дробно-рациональной функции является элементарной функцией, которая выражается с помощью многочлена, дробно-рациональной функции, логарифма и арктангенса.
