Подстановки Эйлера, играя важную теоретическую роль, на практике приводят обычно к громоздким выкладкам, поэтому прибегать к ним надо в крайних случаях, когда не удается более просто вычислить интеграл другим способом. Одним из таких способов является следующий. Если в квадратном трехчлене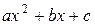 
выделить полный квадрат, то есть привести его к виду
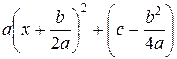и положить 
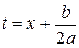, то интеграл
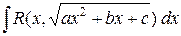приводится к одному из трех видов:
, 
, 
.
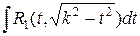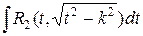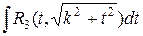Сделав в первом из этих интегралов подстановку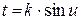 
, во втором
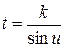, в третьем 
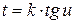, получаем интегралы вида 
.
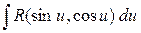Способы их вычисления будут рассмотрены в следующем параграфе.
Пример 6.Вычислить интеграл 
.
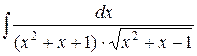Выделим полный квадрат в подкоренном выражении:
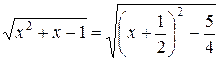.Сделаем замену 
.
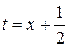Подставляя в исходный интеграл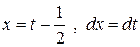 
, получаем
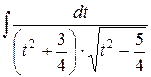.В этом интеграле делаем замену 
,
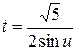приэтом мы избавляемся от иррациональности, так как
, 
.
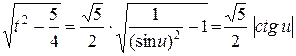
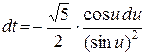Подставляя эти выражения в интеграл в случае, если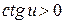 
, затем упрощая подынтегральное выражение, получаем
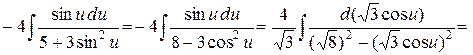
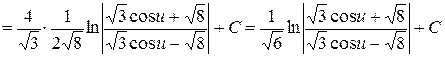, где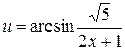 
.
Возвращаясь к первоначальной переменной, получаем
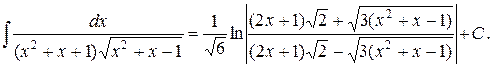
Аналогично интеграл вычисляется в случае, если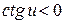 
.
