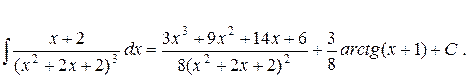Рассмотрим случай, когда дробь правильная, то есть степень многочлена в числителе меньше, чем степень многочлена в знаменателе. Более того, дробь является простейшей. Простейшие дроби бывают четырёх типов:
; 
; 
;
.
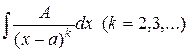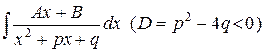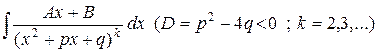Интегралы от простейших дробей первого и второго типа почти табличные
;
.
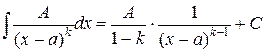Вычислим интеграл от простейшей дроби третьего типа. Вычисление этого интеграла состоит из нескольких этапов:
1) Сначала выделяем полный квадрат в знаменателе дроби
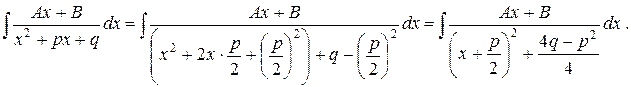
Так как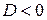 
, то можно переобозначить константу 
.
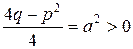2) Делаем замену переменной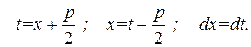 
Получаем интеграл 
.
3) Поделив дробь почленно, разбиваем на два интеграла. Первый из них интегрируется внесением под дифференциал, а второй является табличным.
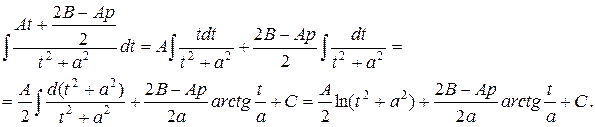
4) Возвращаясь к старой переменной, получаем
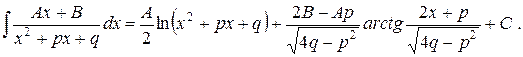
Интеграл от простейшей дроби четвертого типа вычисляется аналогично интегралу от простейшей дроби третьего типа. Кроме того, для интегрирования простейшей дроби четвертого типа нужно использовать рекуррентную формулу. Выделив в знаменателе полный квадрат, сделав замену переменной 
, переобозначив 
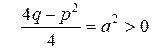и разбив на два интеграла, получаем
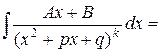
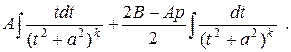
Первый интеграл вычисляется внесением под дифференциал, а второй необходимо считать по рекуррентной формул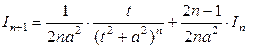е 
, где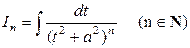 
.
Пример.Вычислить интеграл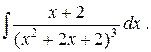 
Выделим полный квадрат и сделаем замену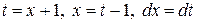 
:
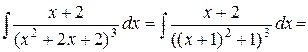
Применив рекуррентную формулу при n=2, затем при n=1, получаем
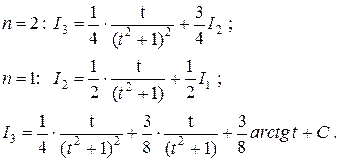
Подставив найденное значение для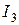 
, 
и вернувшись к старой переменной, находим значение искомого интеграла
