Приведем алгоритм вычисления интеграла от произвольной рациональной функции.
1) Определяем, дробь правильная или неправильная. В случае если дробь неправильная, то есть степень многочлена в числителе не меньше, чем степень многочлена в знаменателе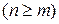 
, выделяем целую часть и представляем неправильную дробь в виде суммы многочлена и правильной дроби
.
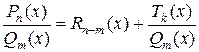2) Для того, чтобы проинтегрировать правильную дробь:
1. Знаменатель раскладываем на множители: линейные, или квадратичные, с отрицательным дискриминантом
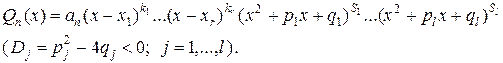
2. Правильную дробь представляем в виде суммы простых дробей с неопределёнными коэффициентами
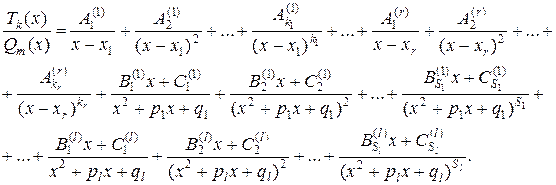
3. Далее находим неопределённые коэффициенты (одним из двух ранее рассмотренных способов)
3) Вычисляем интегралы от простых дробей так, как описано в предыдущем пункте 3.1.
Пример.Вычислить интеграл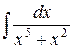 
.
Подынтегральная дробь правильная. Раскладываем ее знаменатель на множители, по этому разложению выписываем представление правильной дроби в виде суммы простейших дробей с неопределенными коэффициентами
.
Домножаем это равенство на знаменатель
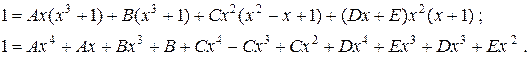
Затем приравниваем коэффициенты при соответственных степенях переменной и решаем полученную систему
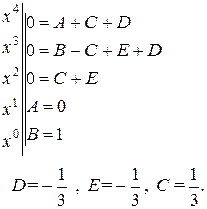
Подставим найденные коэффициенты и получим представление искомого интеграла в виде суммы трех слагаемых.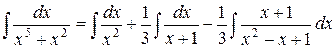 
Первые два интеграла табличные, а последний интеграл от простейшей дроби третьего типа. Вычислим его по описанному ранее алгоритму.
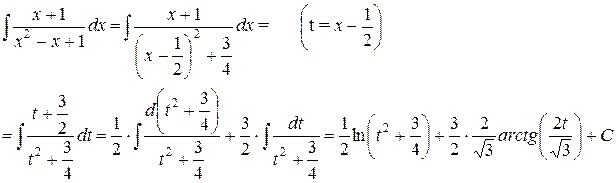
Итак, в результате искомый интеграл равен
.
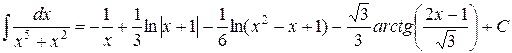