Для любого комплексного числа 
можно определить его модуль по формуле: 
.
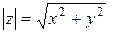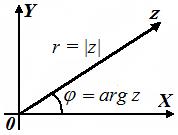Геометрический смысл модуля: модуль – это расстояние между началом координат и точкой 
, соответствующей числу .
Свойства модуля:
1) 
;
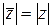2) 
;
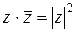3) 
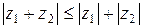– неравенство треугольника;
4) 
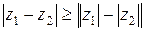– обратное неравенство треугольника.
Определение. Аргументом комплексного числа называется угол, между положительным направлением оси OX и радиус-вектором числа z.
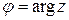– главное значение аргумента, этот угол изменяется в промежутке 
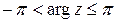. Он вычисляется по формуле
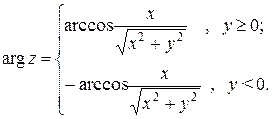
Произвольный угол, соответствующий данному комплексному числу, принадлежит множеству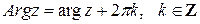 
.
Заметив, что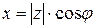 
и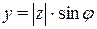 
, и подставив эти выражения
в алгебраическую форму записи комплексного числа, получим тригонометрическую форму записи комплексного числа
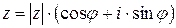
Пример1.Записать комплексное число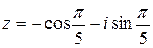 
в тригонометрической форме 
.
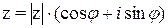Действительная и мнимая части этого числа равны соответственно
, 
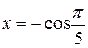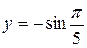. Найдем модуль 
.
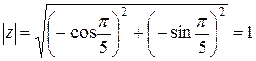Так как мнимая часть отрицательна, то аргумент находится по формуле 
Получаем тригонометрическую форму записи:
.
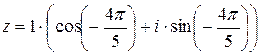В тригонометрической форме записи удобно выполнять действия : умножение, деление, возведение в степень и извлечение корня.
Чтобы умножить два комплексных числа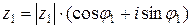 
и
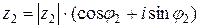в тригонометрической форме записи, нужно их модули перемножить, а аргументы сложить: 
.
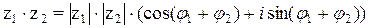Доказательство.
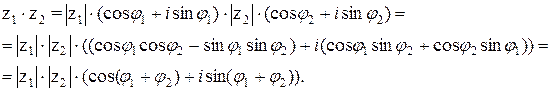
Чтобы поделить два комплексных числа 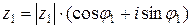и 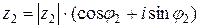в тригонометрической форме записи, нужно их модули поделить, а аргументы вычесть.
.
.
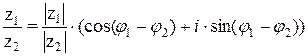