Рассмотрим множество 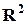 , элементами которого являются пары
, элементами которого являются пары  , где
, где 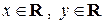 . Введём в этом множестве арифметические действия.
. Введём в этом множестве арифметические действия.
Действие сложение между элементами 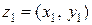 и
и 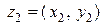
 определяется следующим образом:
определяется следующим образом:  и обладаетсвойствами:
и обладаетсвойствами:
1) ассоциативность  ;
;
2) существование нулевого элемента 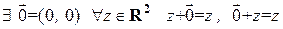 ;
;
3) существование противоположного элемента  ;
;
4) коммутативность 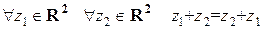 .
.
Действие умножение между элементами 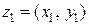 и
и 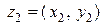
определяется следующим образом  и обладаетсвойствами:
и обладаетсвойствами:
1) ассоциативность 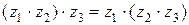 ;
;
2) существование единичного элемента
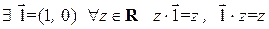 ;
;
3) существование обратного элемента 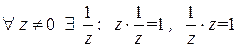 ;
;
4) коммутативность 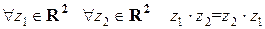 .
.
Имеет место также свойство дистрибутивности
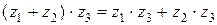 .
.
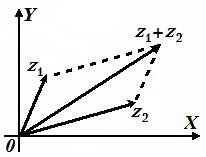
Комплексное число можно изображать либо точкой на плоскости, либо вектором. Если ввести для единичных векторов обозначения 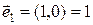 и
и 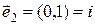 , а также если учесть, что
, а также если учесть, что 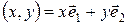 , то любое комплексное число можно записать в виде:
, то любое комплексное число можно записать в виде:
 - алгебраическая форма записи комплексного числа.
- алгебраическая форма записи комплексного числа.
При этом действительное число x называется действительной частью комплексного числа z и обозначается x = Re z, а действительное число y называется мнимой частью комплексного числа z и обозначается y = Im z .
Заметим, что 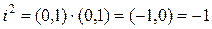 . Тогда умножение комплексных чисел в алгебраической форме можно производить, просто раскрывая скобки:
. Тогда умножение комплексных чисел в алгебраической форме можно производить, просто раскрывая скобки:

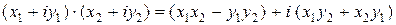
Комплексное число 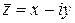 называется
называется
сопряженным числом к числу  .
.
Действие деление между элементами 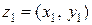
и 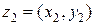 определяется следующим образом:
определяется следующим образом:
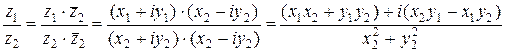
Свойства сопряжённых чисел
1) 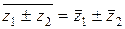 ;
;
2) 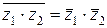 ;
;
3) 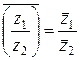
 .
.