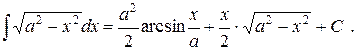Теорема.Пусть X, Y, Z – промежутки, и заданы функции 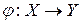 ,
,  . При этих условиях определена композиция
. При этих условиях определена композиция 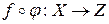 ,
,  . Пусть функция
. Пусть функция  дифференцируема на промежутке X, и функция
дифференцируема на промежутке X, и функция  имеет первообразную
имеет первообразную  на промежутке Y. Тогда
на промежутке Y. Тогда 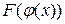 – первообразная для функции
– первообразная для функции  на промежутке X, то есть справедливы формулы:
на промежутке X, то есть справедливы формулы:
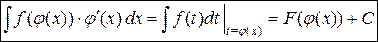 – формула замены переменной;
– формула замены переменной;
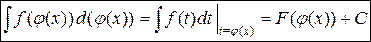 –
– 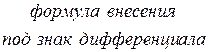 .
.
Доказательство. По правилу вычисления производной от сложной функции имеем
ЗДЕСЬ
 . Это означает, что функция
. Это означает, что функция  является первообразной для функции
является первообразной для функции  . Тогда по определению неопределенного интеграла имеем:
. Тогда по определению неопределенного интеграла имеем:
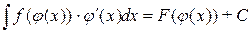 и
и 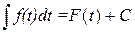 .
.
Так как  , то формула доказана.
, то формула доказана.
Пример 1.Вычислить интеграл  .
.
Воспользуемся приемом внесения под дифференциал.
Так как 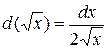 , то
, то
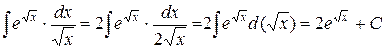 .
.
Пример 2.Вычислить интеграл 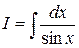 .
.
Решим этот пример двумя способами.
1 способ (внесение под дифференциал).
Домножим на  числитель и знаменатель дроби
числитель и знаменатель дроби
 .
.
Применив формулу 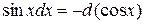 , получаем табличный интеграл.
, получаем табличный интеграл.
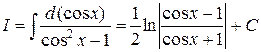 .
.
Ответ можно упростить, пользуясь тригонометрическими формулами понижения степени
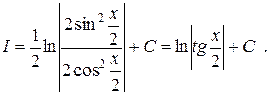
2 способ (универсальнаяподстановка).
Из курса тригонометрии известны формулы
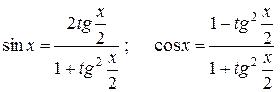 .
.
Сделаем замену 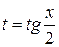 . Тогда
. Тогда
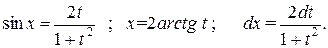
Подставляя эти выражения в первоначальный интеграл, получаем

Пример 3.Вычислить интеграл 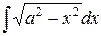 .
.
Сделаем замену
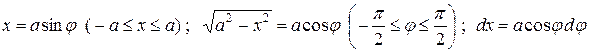 .
.
Применяя формулу  понижения степени, получаем
понижения степени, получаем
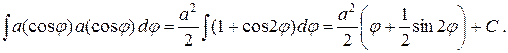
Вернемся к первоначальной переменной
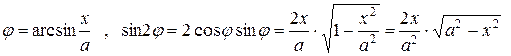 .
.
Тогда получаем окончательный ответ