Нахождение неопределенных интегралов.
Краткие теоретические сведения.
I. Определение и основные свойства неопределенного интеграла.
Определение. Функция F(x) называется первообразной для функции f(x) на множестве Х, если для любого элемента х множества Х F¢(x)= f(x).
Множество всех первообразных функций F(x)+С называют неопределенным интегралом и обозначают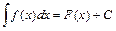 
. f(x) называют подынтегральной функцией, f(x)dx подынтегральным выражением, х– переменной интегрирования. Операция нахождения неопределенного интеграла от функции f(x) называется интегрированием функции f(x).
Свойства неопределенного интеграла:
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению: 
, производная интеграла равна подынтегральной функции: 
.
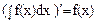2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и некоторой постоянной величины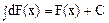 
.
3. Пусть а – некоторое отличное от нуля число, тогда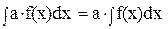 
. (Постоянный множитель можно выносить за знак интеграла).
4. 
. (Интеграл суммы равен сумме интегралов).
Пусть "j=1,2,…,n Aj¹0. Тогда имеет место равенство: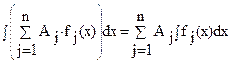 
.
