Для этого приёма характерно многообразие вариантов замены какой-либо функции, входящей в подынтегральную функцию. Удача чаще всего приходит только в случае перебора нескольких вариантов.
Пример 4.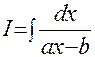 
.
Рецепт. Здесь безальтернативный вариант замены: 
. Это – табличный интеграл: 
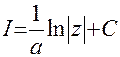. Обратная подстановка 
приводит к конечному результату: 
.
Пример 5.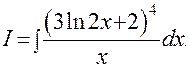 
Рецепт. Опытный взгляд обнаружит интересную дробь 
─ дифференциал функции 
, а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену: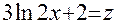 
. Тогда 
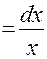
. В результате этой подстановки имеем табличный интеграл: 
. Обратная подстановка приводит к конечному результату 
.
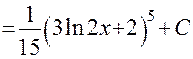К этой же группе интегралов, требующих замены функции, относятся такие, в составе которых имеются радикалы 
ой степени 
, т.е. компоненты типа 
. Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
Пример 6.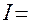 
.
Рецепт. Здесь 
. Очевидна замена 
= 
тогда 
= 
. Тогда интеграл легко приводится к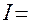 
= = 
+С.
Обратная подстановка даёт конечный результат: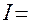 
= 
+С.
