Для любых векторов для любых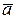 
, 
, 
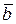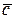и для любого числа 
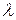справедливо:
1. 
;
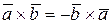2. 
;
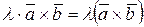3. 
;
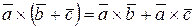4. 
;
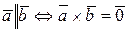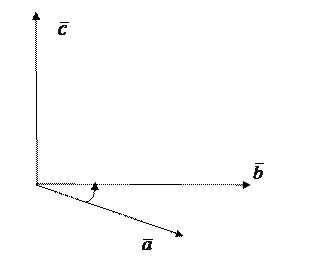
5. Таблица умножения ортов:
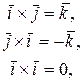
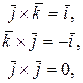
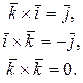
6. Если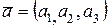 
, 
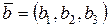, то
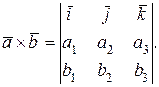
Векторное произведение часто используют для нахождения площадей.
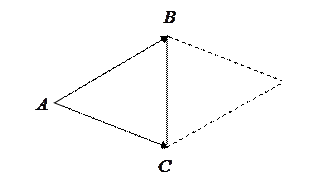
Пример 5. Найти площадь треугольника с вершинами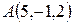 
, 
, 
.
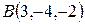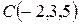Решение. Найдем координаты векторов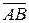 
и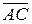 
(напомним, что для этого нужно из координат конца вектора вычесть координаты начала):
, 
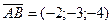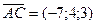
Учитывая, что норма векторного произведения векторов 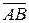и 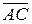численно равна площади параллелограмма, построенного на этих векторах (рис. 2), для нахождения площади треугольника достаточно будет площадь параллелограмма разделить на два.
,
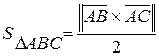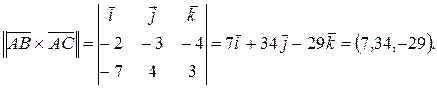
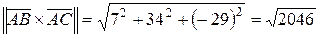
Таким образом,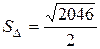 
.n
