Для любых векторов 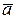 ,
, 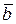 и
и 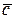 справедливо:
справедливо:
1) При перестановке местами двух множителей смешанное произведение меняет знак:
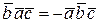 ,
, 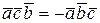 ,
, 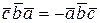
2) При циклической перестановке множителей смешанное произведение не меняется:
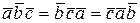 .
.
3) Если 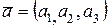 ,
, 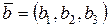 ,
, 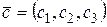 , то
, то
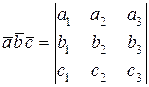 .
.
4) 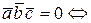
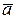 ,
, 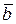 и
и 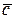 компланарны, т.е. лежат в одной плоскости.
компланарны, т.е. лежат в одной плоскости.
5) Абсолютная величина смешанного произведения векторов равна объему параллелепипеда, построенного на этих векторах

Объем пирамиды, построенный на тех же векторах в 6 раз меньше:
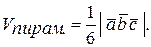
Таким образом, скалярное произведение используют для нахождения длин и углов, векторное произведение – для вычисления площадей, а смешанное – для нахождения объемов.
Пример 6.(Образец выполнения задачи 4 из контрольной работы). Даны вершины пирамиды: 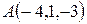 ,
, 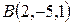 ,
, 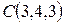 и
и 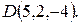
 Найти:
Найти:
a) длину ребра 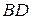 ;
;
b) угол между ребрами 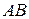 и
и 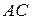 ;
;
c) площадь грани 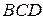 ;
;
d) объем пирамиды.
Решение.
a) Найдем вектор 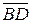 , а затем его норму. Это и будет длина ребра
, а затем его норму. Это и будет длина ребра 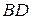 .
. 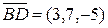 ,
, 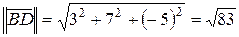
b) Угол между ребрами 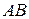 и
и 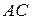 будем находить как угол между векторами
будем находить как угол между векторами 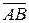 и
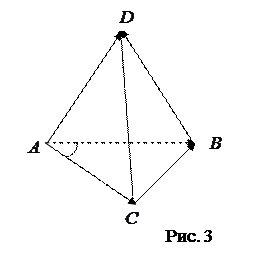
и 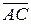 (рис. 3), используя формулу:
(рис. 3), используя формулу:
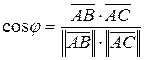 .
.
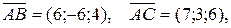
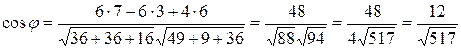 .
.
Следовательно, 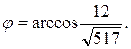
c) 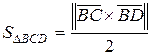 ,
, 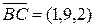 ,
, 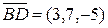
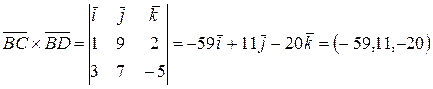
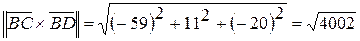 ,
, 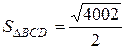 .
.
d) Возьмем три вектора, на которых построена пирамида, например, 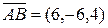 ,
, 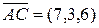 и
и 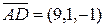 , и найдем их смешанное произведение:
, и найдем их смешанное произведение:
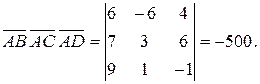
Значит, 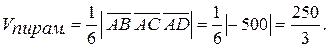 n
n