Для любых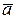 
, 
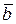и для любого числа 
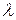справедливо:
1. 
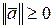, причем 
;
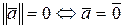2. 
;
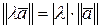3. 
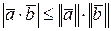- неравенство Коши-Буняковского;
4. 
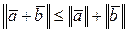- неравенство треугольника;
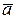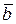Углом между векторами и называется число 
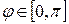, определяемое равенством:
.
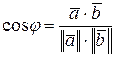Откуда следует , что:
,
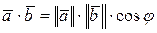т.е. скалярное произведение двух векторов равно произведению длин этих векторов на косинус угла между ними. В этом состоит геометрический смысл скалярного произведения.
Векторы 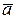и 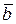называются ортогональными (перпендикулярными), если угол между ними 
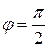. Значит,
.
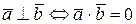Пример 4. При каком значении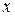 
векторы 
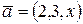и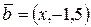 
ортогональны?
Решение.
,
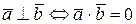т.е.
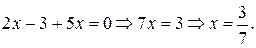
Ответ: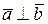 
при 
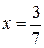.n
