Матрицы умножаются по правилу «строка на столбец». Расшифруем, что имеется в виду.
Произведением матрицы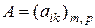 
на матрицу 
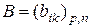называется матрица 
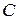размера 
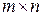с элементами 
, 
, 
.
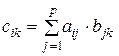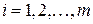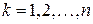Другими словами, для получения элемента, стоящего в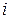 
-той строке и 
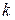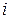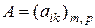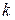-том столбце матрицы-произведения, следует вычислить сумму произведений элементов -той строки матрицы на -тый столбец матрицы .
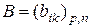В самом определении произведения матриц заложено, что число столбцов первой матрицы должно совпадать с числом строк второй. Это условие согласования матриц при умножении. Если оно нарушено, то матрицы перемножить нельзя.
Пример 2. Найти произведение матриц 
и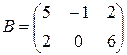 
.
Решение.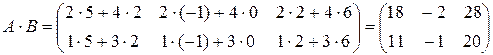 
.n
Заметим, что вполне возможна ситуация, когда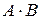 
существует, а 
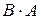нет. Именно так происходит в примере 2. Кроме того, когда существуют оба произведения, то чаще всего они не равны, т.е., вообще говоря, 
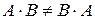. Приведем еще ряд свойств операции умножения матриц. Есл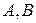и 
и 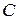- квадратные матрицы одного порядка, то справедливы равенства:
;
;
;
.