Представим систему линейных уравнений с n неизвестными в матричном виде. Пусть
А – матрица, составленная из коэффициентов при неизвестных (её называют основной матрицей системы),
Х – матрица-столбец неизвестных
В – матрица-столбец свободных членов.
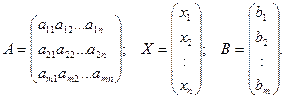
Тогда систему (1) можно записать при помощи этих матриц следующим образом:
A× Х=В (2)
Действительно,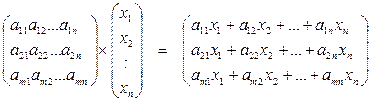 
Уравнение (2) равносильно системе (1).
Матричная запись системы (1) аналогична записи уравнения с одним неизвестным ax=b, решением которого при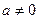 
будет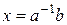 
. Естественно поставить аналогичный вопрос для решения матричного уравнения A × Х=В.
Если матрица А – невырожденная, т.е. detA ≠ 0 и А имеет единственную обратную матрицу А-1, то Х = А-1 В – решение системы уравнений (1).
Пример.
Решите систему матричным методом
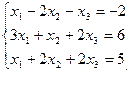
Решение:
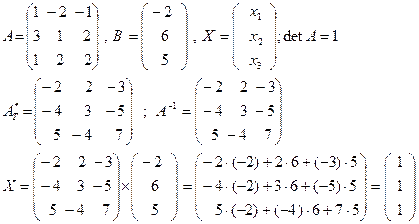
Ответ: (1; 1; 1)
