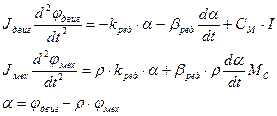Исследование нелинейной двухмассовой разомкнутой системы
По дисциплине Электромеханические Системы
Выполнила: ст. гр. АУ-1-04
Симонина И.А.
Принял: асс. Овчинников А. П.
Москва 2008
Расчётная схема двухмассовой электромеханической системы (момент нагрузки приложен к валу исполнительного механизма)
Составим уравнения, описывающие механическую часть этой системы. Эти уравнения будем составлять в виде уравнений Лагранжа второго рода. За обобщённые координаты примем угол поворота вала двигателя jдвиг и исполнительного механизма jмех. Запишем выражение для кинетической энергии данной системы:
В этом выражении Jдвиг Jмех – моменты инерции якоря двигателя и исполнительного механизма соответственно.
Вычислим производные от этой энергии:
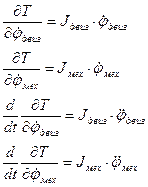
Запишем выражения для потенциальной энергии системы. Как известно, потенциальная энергия деформации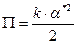 
, где
k – физическая жёсткость медленного вала, 
,
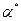- действительная крутильная деформация упругого вала, 
.
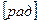Для системы:
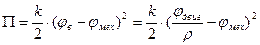
Вычислим производные от этой энергии:
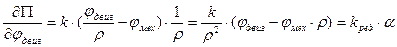
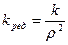- жесткость валопровода, приведённая к валу двигателя.
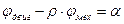- угол деформации валопровода, приведённый к валу двигателя.
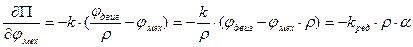
Работа обобщённой неконсервативной силы:
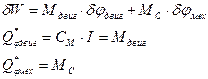
Уравнения для механической части системы без учёта диссипативных сил:
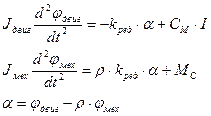
Учтём работу диссипативной силы:
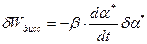
Заменим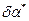 
перемещение в схеме с приведёнными параметрами
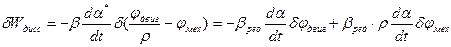
Тогда
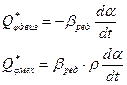
И окончательно, система уравнений, описывающая механическую часть системы с учетом диссипативной силы, принимает вид:
