Интегральная формула Муавра-Лапласа используется для нахождения вероятности 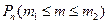 того, что событие А наступит не менее
того, что событие А наступит не менее 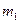 раз и не более
раз и не более  раза при достаточно большом числе n независимых повторных испытаний.
раза при достаточно большом числе n независимых повторных испытаний.
Интегральная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность 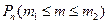 того, что событие А наступит не менее
того, что событие А наступит не менее 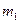 раз и не более
раз и не более  раза в n независимых повторных испытаниях при достаточно большом числе n, приближенно равна
раза в n независимых повторных испытаниях при достаточно большом числе n, приближенно равна
 , (1)
, (1)
где 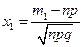 и
и  , а
, а  - функция Лапласа в точке х.
- функция Лапласа в точке х.
Чем больше n, тем точнее приближенная формула (1), называемая локальной формулой Муавра-Лапласа.
Значения функции Лапласа находятся по специальной таблице. При использовании таблицы необходимо учесть:
1) функция 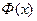 является нечетной, т.е.
является нечетной, т.е. 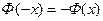 ;
;
2) функция  при
при 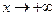 (практически можно считать, что
(практически можно считать, что 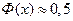 при
при  ).
).
Пример. По данным примера предыдущего параграфа найти вероятность того, что стрелок попадет по мишени не менее 75 раз и не более 90 при 100 выстрелах.
Решение. По условию задачи 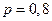 ,
,  ,
,  ,
, 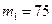 ,
,  .
.
Сначала определим значения
 и
и 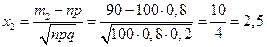 .
.
По формуле (1) получим

 .
.
Здесь учтено, что функция 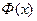 является нечетной. Значения функции
является нечетной. Значения функции 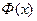 найдены по таблице:
найдены по таблице: 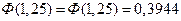 ,
, 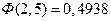 .
.