Рассмотрим следствие интегральной теоремы Муавра-Лапласа.
Следствие. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что относительная частота 
события А будет отличаться от его вероятности р по абсолютной величине не более, чем на величину 
, при достаточно большом числе n независимых повторных испытаний определяется по формуле
. (1)
Доказательство: Рассмотрим неравенство 
. Данное неравенство эквивалентно неравенству
или 
.
Так как относительная частота события определяется как 
, где n – число проведенных испытаний, m – число испытаний, в которых наступило событие А, то имеем неравенство
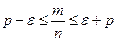Û
.
Таким образом, неравенство эквивалентно неравенству . Тогда равны вероятности выполнения этих неравенств, т.е.
.
Используя интегральную формулу Муавра-Лапласа, получим
,
что и требовалось доказать.
Пример. Сколько раз нужно подбросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты выпадений герба от вероятности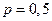 
окажется по абсолютной величине не более 0,01?
Решение. По условию задачи вероятность выпадения герба в каждом испытании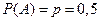 
, 
, а 
. Тогда из неравенства (1) имеем: 
или 
. По таблице значений функции Лапласа получим, что значению функции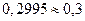 
соответствует значение аргумента 
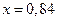. Следовательно, 
Þ 
Þ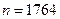 
. Таким образом, монету необходимо подбросить 1764 раза.
