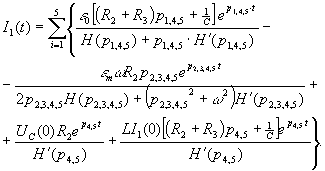
| Пусть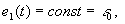 
 . В момент t = 0 размыкается ключ и вместо него подключается сопротивление 
|
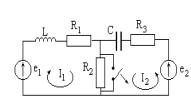
Составим уравнения для двух контуров по методу контурных токов в операторной форме.
.
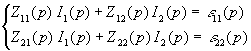Здесь 
,
,
, 
, 
.
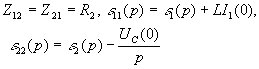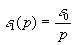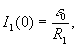
Начальные значения тока в индуктивности и напряжения на емкости
, ,
.
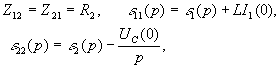
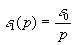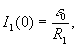
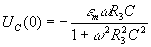Начальные значения тока в индуктивности и напряжения на емкости определяются при замкнутом ключе, так как при его размыкании они изменяться не могут. 
определяется непосредственно. Для комплексной амплитуды напряжения на емкости можно получить:
где
,
или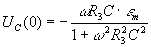 
, т. к.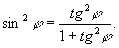 
Решив систему уравнений для контурных токов получим:
; 
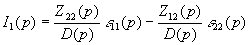, где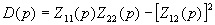 
.
Подставляя сюда значения операторных образов, сопротивлений и ЭДС, получим, например, следующие выражения для тока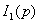 
:
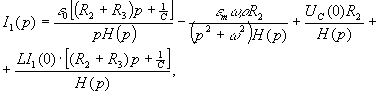
где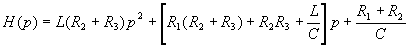 
.
В полученном выражении для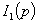 
первые два члена определяют ток в переходном процессе при включении цепи под действием ЭДС е1 и е2.Последние два члена определяют ток переходного процесса, возникающего в цепи за счет ненулевых начальных значений тока в индуктивности Lи напряжения на конденсаторе С. Для перехода к временной зависимости тока с помощью вычетов необходимо найти нули знаменателей: 
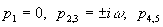определяются решением уравнения 
.
.
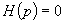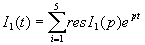При вычислении вычетов от рациональных дробей выражения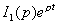 
значения нулей знаменателя 
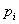поочередно подставляются в числители и производные знаменателей:
