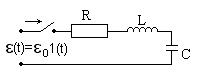
| Пусть в момент времени t = 0 включается постоянное ЭДС 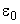 на цепь R, L, C с нулевыми начальными условиями, т. е.I(0) = 0;  .
|
Запишем II уравнение Кирхгофа для мгновенных значений напряжения:
.
Дифференцируя обе части, получим уравнение второго порядка для тока:
.
Обозначив 
для соответствующего однородного уравнения, получим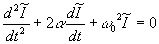 
. Характеристическое уравнение 
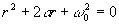имеет корни 
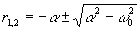, решение однородного уравнения: 
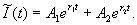Общее решение неоднородного уравнения есть 
, где 
- ток установившегося режима (частное решение). В нашем случае 
, т. к. постоянный ток через емкость пройти не может. Постоянные 
найдем из начальных условий: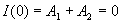 
;
,
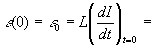
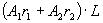т. к. 
.
Тогда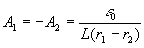 
; 
.
При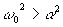 
, т. е. 
, 
; 
,
.
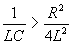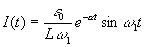Применим к этой задаче операторный метод.
При 
, 
, 
,
.
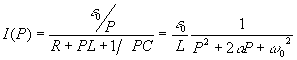Корни знаменателя 
. Найдем вычеты от функции 
, имеющей два полюса первого порядка:
.
Наглядно видное преимущество операторного метода особенно проявляется при расчете сложных цепей.
