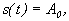1) 
- фильтрующее свойство.
2) Четность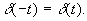 
3) Нормировка 
Спектральная плотность
.
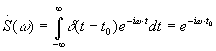При t0 = 0, 
,
при t0 ¹ 0,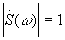 
.
- это спектральное определение d-функции.
Аналогично 
- определение d-функции в частотной области.
Спектральная плотность гармонического колебания
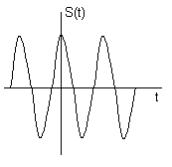
| Одним из условий применения интегрального преобразования Фурье функцииs(t) является ее абсолютная интегрируемость 
Применениеd-функции позволяет получить спектральную плотность и для неинтегрируемых функций.
|
Пусть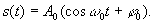 
Найдем спектральную плотность, формально не обращая внимания, что сигнал абсолютно не интегрируем.
Произведем замену 
.
Но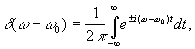 
тогда
.
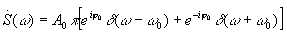Гармоническому колебанию с конечной амплитудой соответствует бесконечно большая спектральная плотность на дискретных частотах ±w0.
В частности, для постоянного напряжения w0 = 0, 
