Найдем спектр квадрата функции s(t).
 - используем свойства преобразования Фурье для произведения двух функций.
- используем свойства преобразования Фурье для произведения двух функций.
В частном случае (  ) будем иметь:
) будем иметь:
 . Переходя от
. Переходя от  к
к 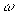 и т. к.
и т. к.  , комплексное сопряженние
, комплексное сопряженние  .
.
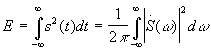 - равенство Парсеваля.
- равенство Парсеваля.
 - спектральная плотность энергии (энергия, приходящаяся на единицу полосы частот). Е - полная энергия сигнала.
- спектральная плотность энергии (энергия, приходящаяся на единицу полосы частот). Е - полная энергия сигнала.
Для энергии, приходящейся на конечную полосу частот, получим:
 - при симметричной
- при симметричной 
Примеры. Спектр Гауссова (колокольного) импульса
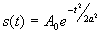 , -¥ < t < ¥, а - условная половина длительности на уровне 0,606.
, -¥ < t < ¥, а - условная половина длительности на уровне 0,606.
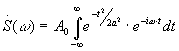 .
.
Произведем преобразование в показателях степени:

где d - определяется из условия:
 откуда
откуда 
 .
.
При d - конечном 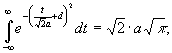 т. к.
т. к. 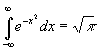 .
.
Тогда  т. е. спектр Гауссова импульса имеет Гауссову форму:
т. е. спектр Гауссова импульса имеет Гауссову форму: 
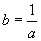 .
.
Можно показать, что Гауссов импульс обладает наименьшим 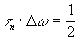 при среднеквадратичном их определении.
при среднеквадратичном их определении.
Спектр d-функции
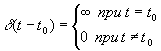 .
.
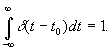
В качестве d-функции может выступать сигнал любой формы с бесконечно малой длительностью и единичной площадью.