Заменим действительную кривую u(t) приближенно ступенчатой с интервалами по оси t, равными Dx. Тогда ток в любой момент времени t можно рассматривать как результат воздействия серии скачкообразных постоянных напряжений, следующих друг за другом через промежутки Dx в интервале от 0 до t.
Скачки напряжения: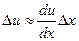 
; 
.
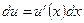Составляющая тока, вызванная отдельным скачком напряжения, действующим в момент x равна
,
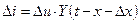где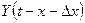 
– переходная проводимость от момента 
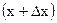возникновения данного скачка напряжения до момента t отсчета значения тока.
Весь ток i(t) является суммой составляющих тока, вызванных отдельными скачками напряжений.
или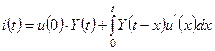 
– интеграл Дюамеля.
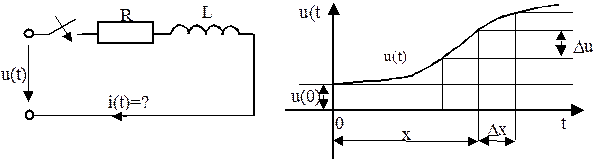
где 
.
Интеграл Дюамеля позволяет решить задачу о включении цепи под действием напряжения u(t) произвольной формы, причем Y(t) определяется в итоге решения более простой задачи – включения той же цепи под действием постоянного напряжения.
Пример:
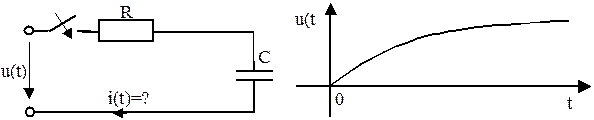
Дано:
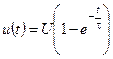, R, C.
Найти:
i(t) – ?
Решение:
1. Определяем Y(t) при включении цепи на постоянном напряжении. Тогда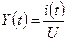 
.
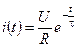
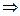
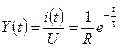2. 
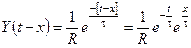
3. 
; 
; 
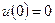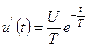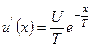
4.
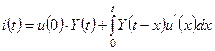
5. 
.
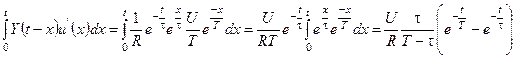