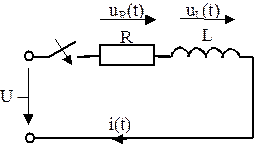
1. На основании законов Кирхгофа для мгновенных значений и с учетом, что 
или ( 
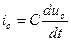) составляем диф. уравнение для послекоммутационной схемы:
.
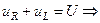
2. Записываем искомое решение: 
.
3. Находим 
(при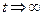 
; 
– подставляем в исходное диф. уравнение и получаем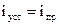 
):
.
4. Находим показатели затухания pk. Характеристическое уравнение:
.
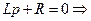
5. 
,
где p – показатель затухания, 
;
A – постоянная интегрирования, А.
Таким образом: 
.
Характеристическое уравнение для определения p часто составляют более простым путём. С этой целью составляют выражение для входного сопротивления цепи на переменном токе [Z(jw)], а затем заменяют в нем jw на p и приравнивают Z(p) нулю:
. Тогда 
.
Важнейшая характеристика переходного процесса 
– постоянная времени:
.
6. Определяем постоянную интегрирования.
6.1.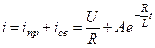 
При 
:
.
6.2.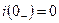 
На основании 1-го закона (правила) коммутации: 
.
6.3. Следовательно 
.
7. Определяем искомую функцию:
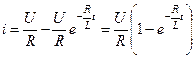
Определяем 
:
;
;
.
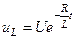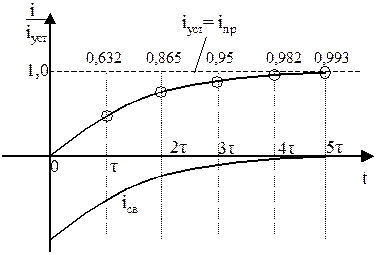
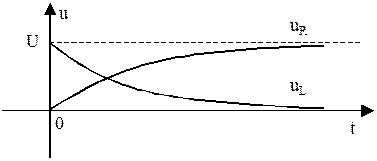
За время t величина i уменьшится в e раз:
| t
|
| τ
| 2 τ
| 3 τ
| 4 τ
| 5 τ
|
| 1–exp(-t/τ)
|
| 0,632
| 0,865
| 0,95
| 0,982
| 0,993
|
| exp(-t/τ)
|
| 0,308
| 0,135
| 0,05
| 0,018
| 0,007
|
Примечание
1. Длительность переходного процесса характеризуется t
Переходный процесс практически завершается через t= (3¸5)t.
2. Длительность переходного процесса определяется только параметрами цепи (R, L, C)
Пример:
U=10 В; R=10 Ом; L=0,01 Гн
;
; 
.
Время, через которое закончится переходный процесс: 
tпер = 5 мс.
