Согласно классическому методу:
полное решение (интеграл) линейного неоднородного диф. уравнения равно сумме частного решения исходного диф. уравнения и общего решенияэтого уравнения при равенстве нулю правой части (однородного диф. уравнения):
.
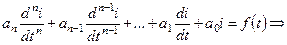
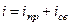Частное решение (одно из решений, удовлетворяющее исходному неоднородному диф. уравнению) определяют путем расчета установившегося режима в послекоммутационной схеме. Эта составляющая переходного тока (напряжения) называется принужденной:
.
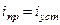Общее решение диф. уравнения без правой части (без источников э.д.с., тока) определяет свободную составляющую переходного тока (напряжения).
Из курса математики известно, что решение однородного линейного диф. уравнения вида
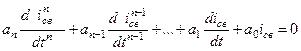
представляет собой сумму экспонент
,
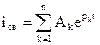где pk – показатели затухания, определяемые как корни характеристического уравнения, полученного из исходного путем замены
; 
; ... ; 
; 
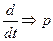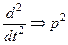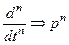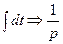
и получения линейного алгебраического уравнения n-ого порядка
;
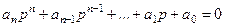Ak – постоянные интегрирования, определяемые по значениям искомой функции и ее производных в момент коммутации (начальные условия).
Начальные условия определяем с помощью законов коммутации.
Действительно: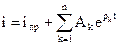 
.
При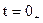 
:
; 
.
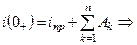
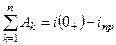
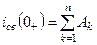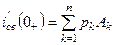Тогда составляем систему из n алгебраических уравнений и находим Ak:
.
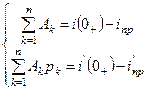