Пример 6.1
Пусть импульсная характеристика пространственного фильтра для формирования плоского скалярного поля имеет вид:
.
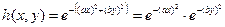Тогда в соответствии с (6.5), получаем:
Заменяем двукратное суммирование двумя однократными скользящими суммированиями:
;
,
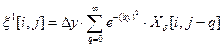где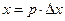 
; 
,
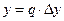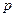и 
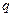- номера отсчетов по осям 
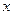и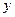 
соответственно;
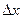- шаг дискретизации по оси ;
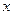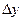- шаг дискретизации по оси .
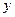Отметим, что при первом суммировании обеспечивается корреляция вдоль оси 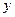, а при втором – вдоль оси .
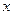6.2 Моделирование случайных полей
с помощью рекуррентных уравнений
Как и ранее при моделировании случайных процессов, рекуррентные уравнения могут быть использованы только для тех случайных полей, спектральная плотность которых может быть представлена в виде дробно-рациональной функции.
Моделирование в этом случае сводится к последовательному применению одномерных алгоритмов фильтрации.
Пусть требуется получить случайное поле, имеющее корреляционную функцию вида:
.
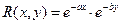1) Сформируем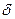 
-поле нужной размерности и заполняем его независимыми отсчетами с нормальным законом распределения 
.
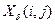2) С помощью алгоритмов моделирования случайных процессов (в данном случае с экспоненциальной корреляционной функцией) производим фильтрацию вдоль оси :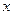
;
.
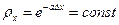3) Производим аналогичную процедуру фильтрации вдоль оси :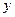
;
.
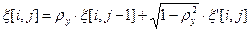4) Делаем нормировку по математическому ожиданию и среднеквадратическому отклонению.
