Пусть требуется получить алгоритм формирования случайной величины, имеющей следующий закон распределения (нормальное распределение с выбросами на концах):
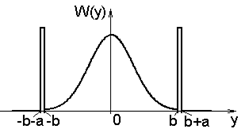
Рис. 2.5 Нормальное распределение с выбросами на концах
Разобьем интервал определения случайной величины 
на 3 подынтервала: 
, 
, 
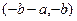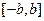. Вероятности попадания случайной величины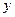 
в крайние подынтервалы будут одинаковы и равны:
.
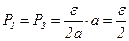Вероятность попадания в центральный подынтервал будет равна:
.
На шаге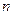 
берем реализацию случайной величины 
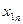равномерно распределенной от 0 до 1 и сравниваем ее с порогами 
и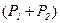 
. Если 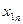не превысила порог , то реализация искомой случайной величины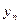 
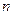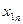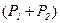на шаге будет находиться в первом подынтервале. Если превысила порог и не превысила порог , то 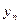будет находиться во втором подынтервале. Если же 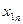превысила оба порога, то 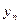будет находиться в третьем подынтервале.
Моделирование случайной величины 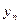в первом и третьем подынтервалах производится с помощью алгоритмов формирования случайных величин с равномерным законом распределения, во втором - с помощью алгоритмов формирования случайных величин с нормальным законом распределения:
,
,
,
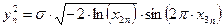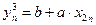где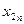 
и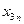 
- случайные величины с равномерным от 0 до 1 законом распределения.
