1. Если функциональный ряд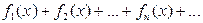 
состоящий из функций, имеющих непрерывные на отрезке [a, b], сходится на этом отрезке к сумме S(x) и ряд 
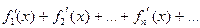, составленный из производных его членов, мажорируем на том же отрезке, то сумма ряда производных равна производной от суммы первоначального ряда, т.е.
.
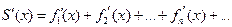2. Пусть имеется ряд непрерывных функций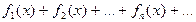 
, мажорируемый на отрезке [a, b], и пусть S(x) есть сумма этого ряда. Тогда интеграл от S(x) в пределах от 
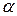до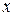 
, принадлежащих отрезку [a, b], равняется сумме таких же интегралов от членов данного ряда, т.е.
.
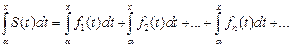Теорема Абеля: 1) Если степенной ряд сходится при некотором значении х0, не равном 0, то он абсолютно сходится при всяком значении х, для которого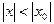 
; 2) если ряд расходится при некотором значении y0, то он расходится при всяком х, для которого 
.
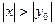