Функция F(x) называется первообразной для функции f(x) на промежутке (a;b), если для всех xÎ(a;b) выполняется равенство F¢(x) = f(x).
Например, для функции x2 первообразной будет функция x3/3.
Если для F(x) установлено равенство dF(x) = f(x)dx, то F(x) – первообразная для f(x), так как 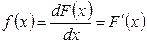 .
.
Вычисление неопределенного интеграла от заданной функции называется интегрированием.
Из определения неопределенного интеграла следует, что каждой формуле дифференциального исчисления F¢(x) = f(x) соответствует формула òf(x) dx = F(x) + C интегрального исчисления. Отсюда получается таблица неопределенных интегралов:
| 1) ò dx = x + C;
| 7) ò cosx dx = sinx + C;
|
2) ò xadx= 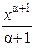 (a¹1); (a¹1);
| 8) 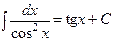 ; ;
|
3) 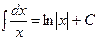 ; ;
| 9) 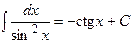 ; ;
|
| 4) ò exdx =ex+C;
| 10) 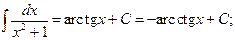
|
| 5) ò axdx =axlogae+C (a¹1) ;
| 11) 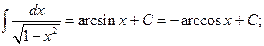
|
| 6) ò sinx dx=-cosx + C;
| 12) 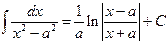 . .
|
Неопределенный интеграл обладает следующими свойствами:
| 1) ( òf(x) dx )¢=f(x);
| 4) òd f(x)=f(x)+C ;
|
| 2) òf¢ (x) dx= f(x)+C ;
| 5) òkf(x)dx=kòf(x) dx;
|
| 3) d òf(x) dx= f(x)dx;
| 6) ò(f(x)+g(x))dx=òf(x) dx+òg(x) dx ;
|
Если òf(x) dx = F(x) + C, то òf(ax+b) dx = 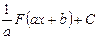 , (a ¹ 0). , (a ¹ 0).
|