Может оказаться что функция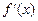 
, называемая первой производной, тоже имеет производную 
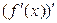. Эта производная называется второй производной функции f(x) и обозначается 
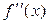. Если f есть координата движущейся точки и является функцией времени, то мгновенная скорость точки в момент времени t равна f¢(t), а ускорение равно f¢¢(t).
Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f¢¢¢(x).
Если определена n-я производная f (n)(x) и существует её производная, то она называется (n+1)-й производной функции f(x): f (n + 1)(x) = (f(n)(x))¢.
Все производные, начиная со второй, называются производными высших порядков.
