1. Если функция имеет производную в точке, то она непрерывна в этой точке.
2. Если существует f¢ (x) , и С ‑ произвольное число, то (Cf(x))¢ = Cf¢ (x).
3. Если существуют f¢ (x) и g¢ (x), то 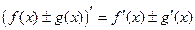 .
.
4. Если существуют f¢ (x) и g¢ (x), то 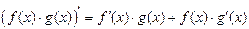 .
.
5. Если существуют f¢ (x) и g¢ (x) и g(x) ¹ 0, то
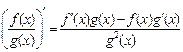 .
.
Пусть функция g(x) имеет производную в точке x, а функция f(z) имеет производную в точке z = g(x). Тогда сложная функция F(x) = f(g(x)) имеет в точке x производную F¢ (x) = f¢ (z) g¢ (x).